Source code is here !

If any of my models ever fit this well I would immediately be suspicious.

Just add more parameters!

This is a lot of jargon to unpack, as someone who isn't fluent in math. Is there an ELI5 for this? Are the graphs saying that an accurately fitting curve is more mathematically congruent overall?

Eventually the function will memorize the training dataset.

4 parameters is enough to fit anything.

https://www.johndcook.com/blog/2011/06/21/how-to-fit-an-elephant/

[deleted]

The objective function really said ( ͡° ͜ʖ ͡°)

I can try the ELI5 (maybe more ELI18) explanation: Curve fitting is nothing but an optimization problem. You try to minimize the residuals (i.e. the squared distances of the searched curve to the training data points).

In the simplest case, your model is linear in the parameters (think polynomials, for example). Most people know the regression line, that is, a line that fits the data points as well as possible. The parameters of such a straight line (and higher-order polynomials) can be estimated in just one step using the OLS estimator.

But here in this case the model is non-linear in the parameters (look at the model function in the first plot) - it is composed of transcendental functions (sine and exp). In such cases, the optimum cannot be found analytically in one step. So we need an iterative approach with gradient descent. There are some methods that can achieve exactly that.

A very classical and simple algorithm is the Gauss-Newton algorithm, but here a modern approach called the Levenberg-Marquardt algorithm was used. The difference is that an underlying optimization problem is solved to determine the search direction.

When your residual error is zero that must mean you've gotten it right!

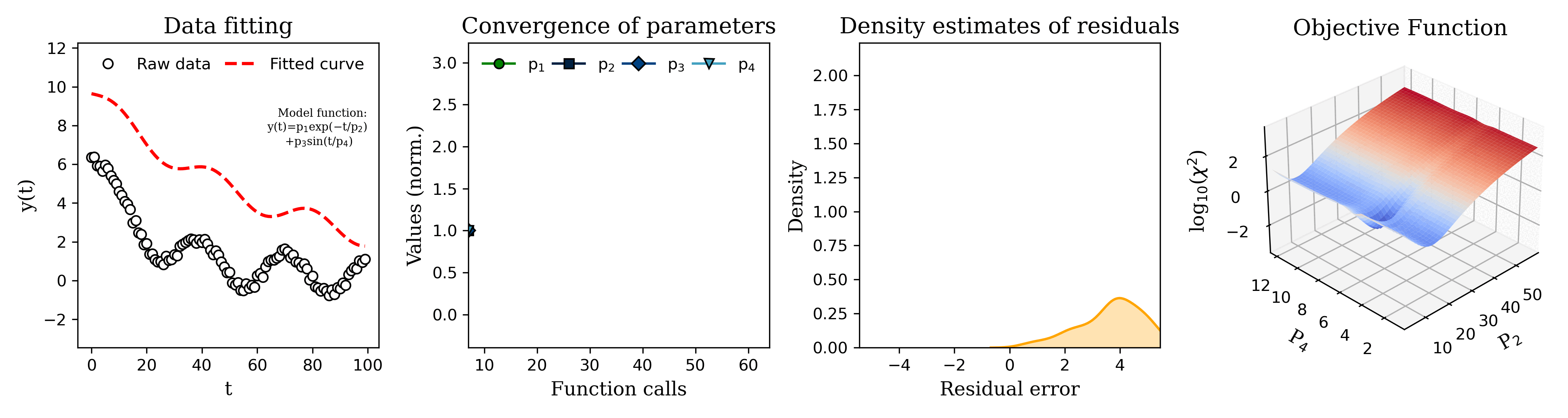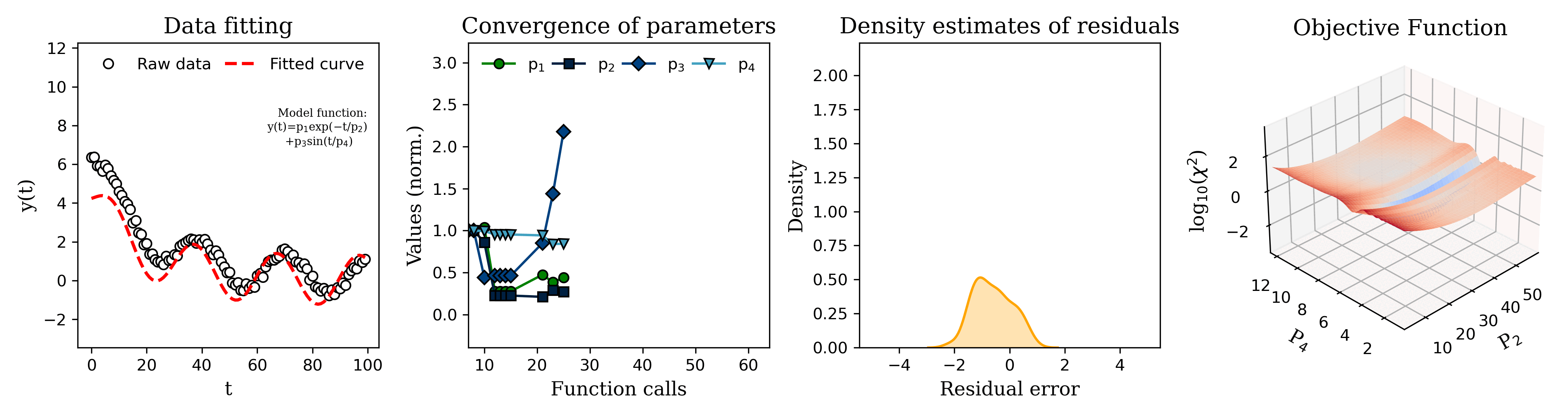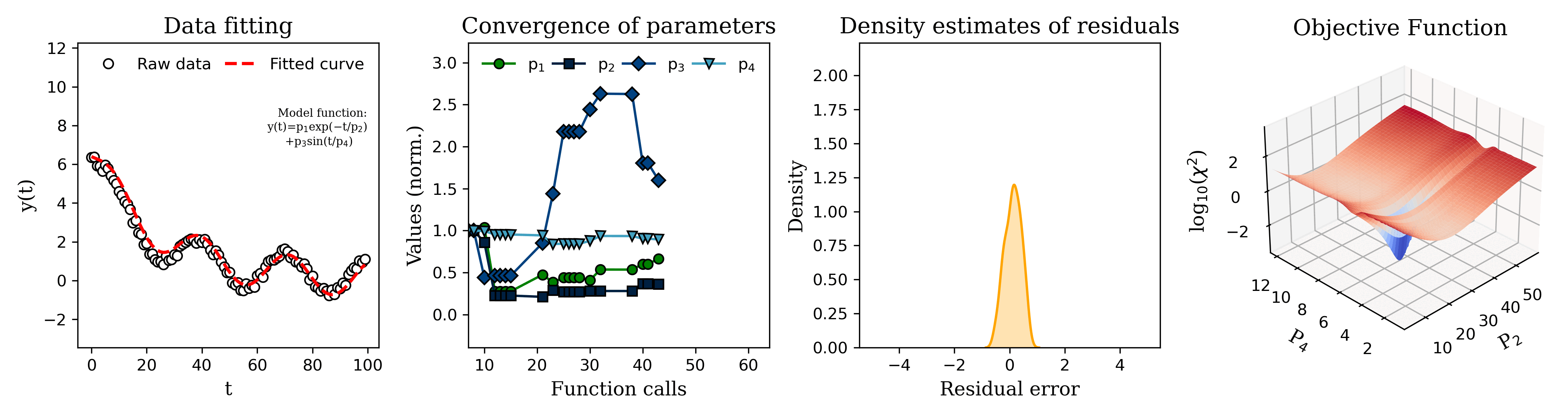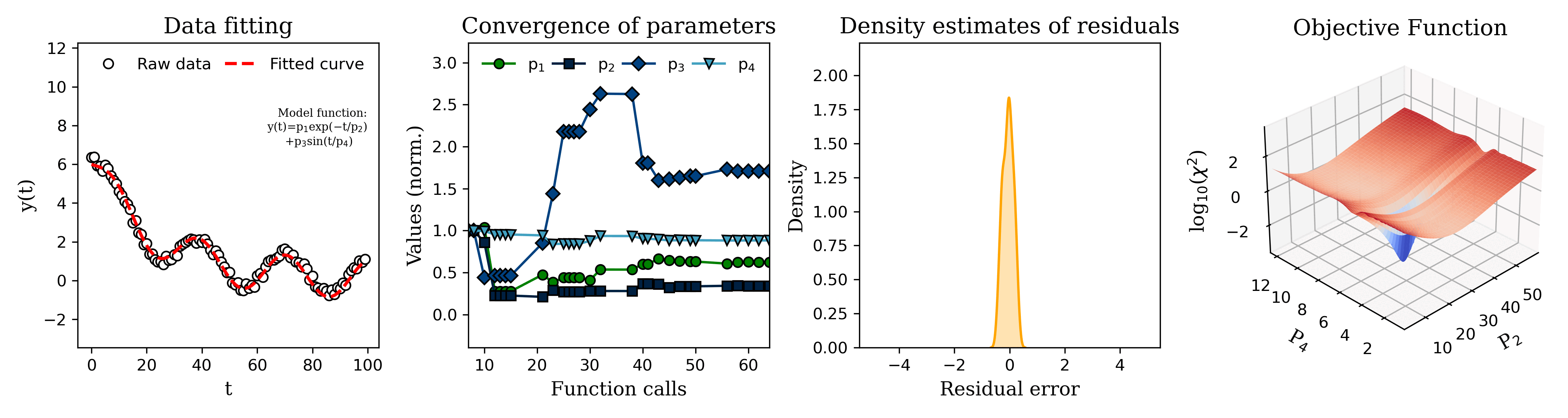
The graphs are just showing the progress of the model-fitting algorithm.

Basically, you give it an equation or set of equations that you think describe the data. These equations contain a number of variables (parameters) whose values are unknown. The algorithm then tries to find the set of parameters that get the equation to match the data.

From left to right, the graphs are:

1. Current model prediction (red dashed line) overlaid on the observed data.

2. Value of the model parameters during each iteration of the fitting algorithm.

3. Distribution of the residual error (error between the model prediction and the observed data) for a given parameter set.

4. Graph of the objective function value (OFV) for a search grid of parameter 2 (P2) and parameter 4 (P4). The OFV is basically a measurement of how well the model matches the data for a given set of parameter values. Often the objective function is constructed such that the better the model fits, the smaller the value of the objective function. So the algorithm tries to minimize the value of the objective function. The downward spike in the center of the graph indicates that those values for P2 and P4 result in a (local) minimum value of the objective function, i.e. those are the parameter values at which the model most closely matches the observed data.

The 'raw data' in the first plot was generated by adding random measurement errors to the model function to simulate artificial measurements :)

Hahaha yep

That's awesome, haven't come across that paper before